Introduction
For mid- to long-distance FPV drone flights, the primary concern is preventing an unexpected battery drop-out. In addition to reliability, optimizing battery selection is crucial for maximizing flight range while balancing weight and performance.
Calculating the optimal capacity
The maximum distance a drone can travel can be estimated using the formula:
$$ \mathrm{distance} = k_{drone} \cdot \frac{\eta \cdot Q}{m_e + \rho \cdot Q} $$ where:
- $\mathrm{distance}$: Maximum travel distance in kilometers (km).
- $k_{drone}$ (Drone Constant): An empirically determined constant reflecting the drone’s aerodynamics and efficiency.
- $Q$ (Battery Capacity): Battery capacity in amp-hours (Ah).
- $\eta$ (Usable Battery Factor): The fraction of the battery’s capacity that can be safely utilized. For example, $\eta = 0.95$ for Li-ion batteries and $\eta = 0.8$ for LiPo batteries.
- $m_e$ (Empty Mass): The drone’s mass without the battery (including payloads like a camera), in kilograms.
- $\rho$ (Battery Mass per Ah): The battery’s weight per amp-hour, which reflects its energy density. For example, $\rho = 1$ for Li-ion and $\rho = 1.4$ for LiPo batteries.
This formula allows you to predict the impact of different battery capacities on your drone’s flight range once you have determined its drone constant, $k_{drone}$.
Determining the Drone Constant $k_{drone}$
To find $k_{drone}$, perform a test flight and record:
- $m$: Total mass of the drone (including the battery), in kg.
- $\mathrm{distance}$: Distance traveled during the test flight, in km.
- $Q_{consumed}$: Battery capacity consumed during the flight, in amp-hours (Ah). (If measured in milliamp-hours, convert by dividing by 1000. For example, 1764 mAh is 1.764 Ah).
If direct measurement of $Q_{consumed}$ is not possible, estimate it using:
- For LiPo batteries: They typically deplete at about 80% of their capacity. E.g., a 1300 mAh battery consumes $1300 \times 0.8 = 1040$ mAh, or 1.04 Ah.
- For Li-ion batteries: They typically deplete at about 95% of their capacity. E.g., a 4000 mAh battery consumes $4000 \times 0.95 = 3200$ mAh, or 3.2 Ah.
Then compute the drone constant using:
$$ k_{drone} = \mathrm{distance} \cdot \frac{m}{Q_{consumed}} $$
To compute your drone’s constants, input these values into the calculator.
For instance, consider a 7-inch drone that flies 12 km with a total mass of 1.345 kg (comprising an empty mass of 0.897 kg and a battery mass of 0.448 kg) and consumes 3.8 Ah. In this case:
$k_{drone} = 12 \cdot 1.345 \div 3.8 = 4.25$.
With $k_{drone}$ established, you can now predict how different battery capacities affect flight distance.
Predicting Flight Distance Using $k_{drone}$
To calculate the flight distance, input the values into the calculator.
Inserting the value of $k_{drone}$ and the appropriate parameters into the distance equation yields predictions for various battery capacities. For a Li-ion battery, where $\eta = 0.95$, $\rho = 1.0$, and the drone’s empty mass $m_e = 0.897$, the equation becomes:
$$ \mathrm{distance} = 4.25 \cdot \frac{0.95 \cdot Q}{0.897 + 1.0 \cdot Q} $$
The total mass of the drone is expressed as:
$$ m = 0.897 + 1.0 \cdot Q $$
| Capacity $Q$ | Distance | Mass |
|---|---|---|
| 4 Ah | 12.4 km | 1.3 kg |
| 6 Ah | 16.2 km | 1.5 kg |
| 8 Ah | 19.0 km | 1.7 kg |
| 12 Ah | 23.1 km | 2.1 kg |
And graphing the distance by the battery capacity, we get:
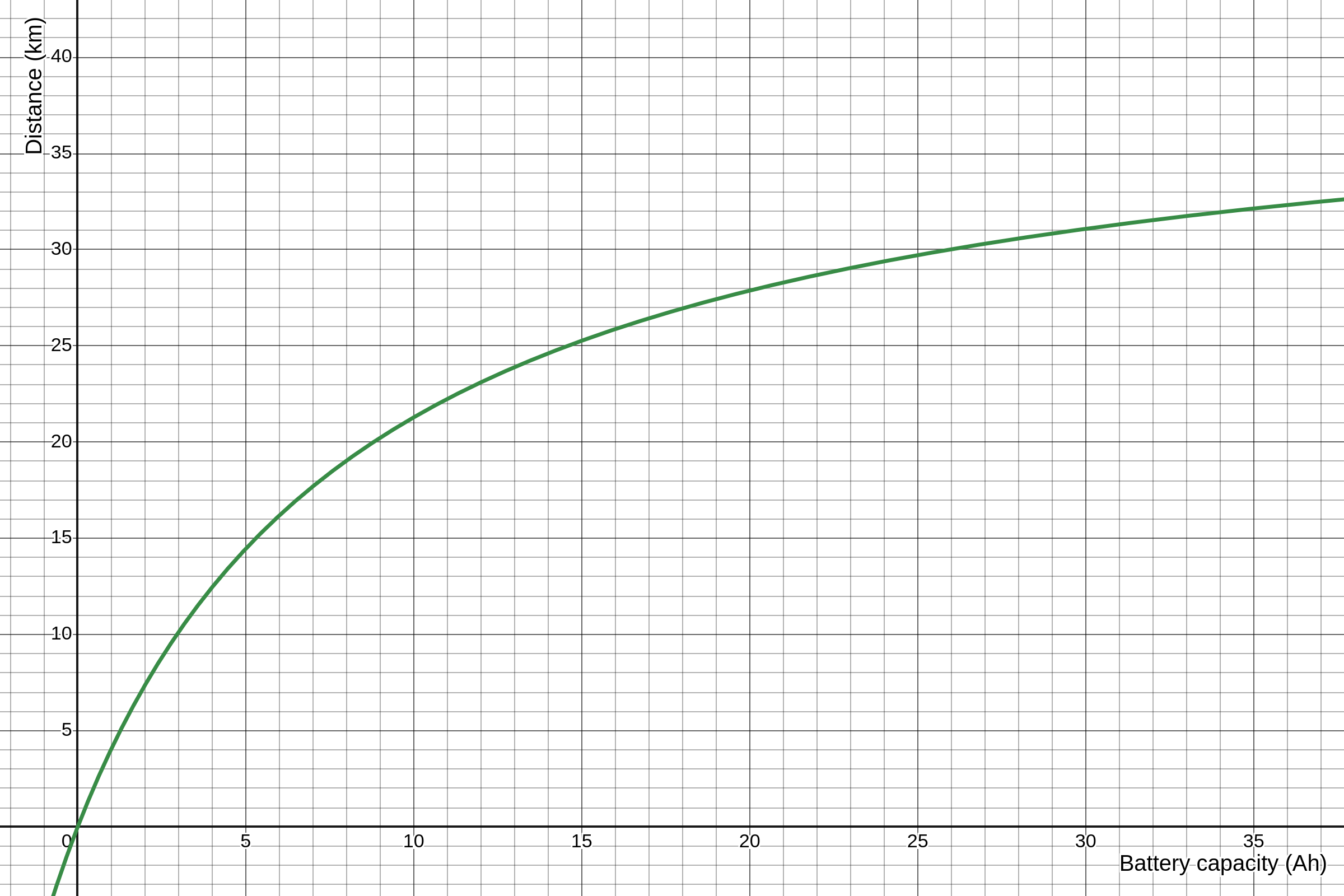
Graphing distance versus battery capacity illustrates diminishing returns after approximately 10 Ah—by which point a range of about 21 km is typically sufficient, especially under local regulations.
For LiPo batteries, with $\eta = 0.8$ and $\rho = 1.4$, the formula adjusts to:
$$ \mathrm{distance} = 4.25 \cdot \frac{0.8 \cdot Q}{0.897 + 1.4 \cdot Q} $$
In green, we have the liion battery, and in violet, the lipo battery.
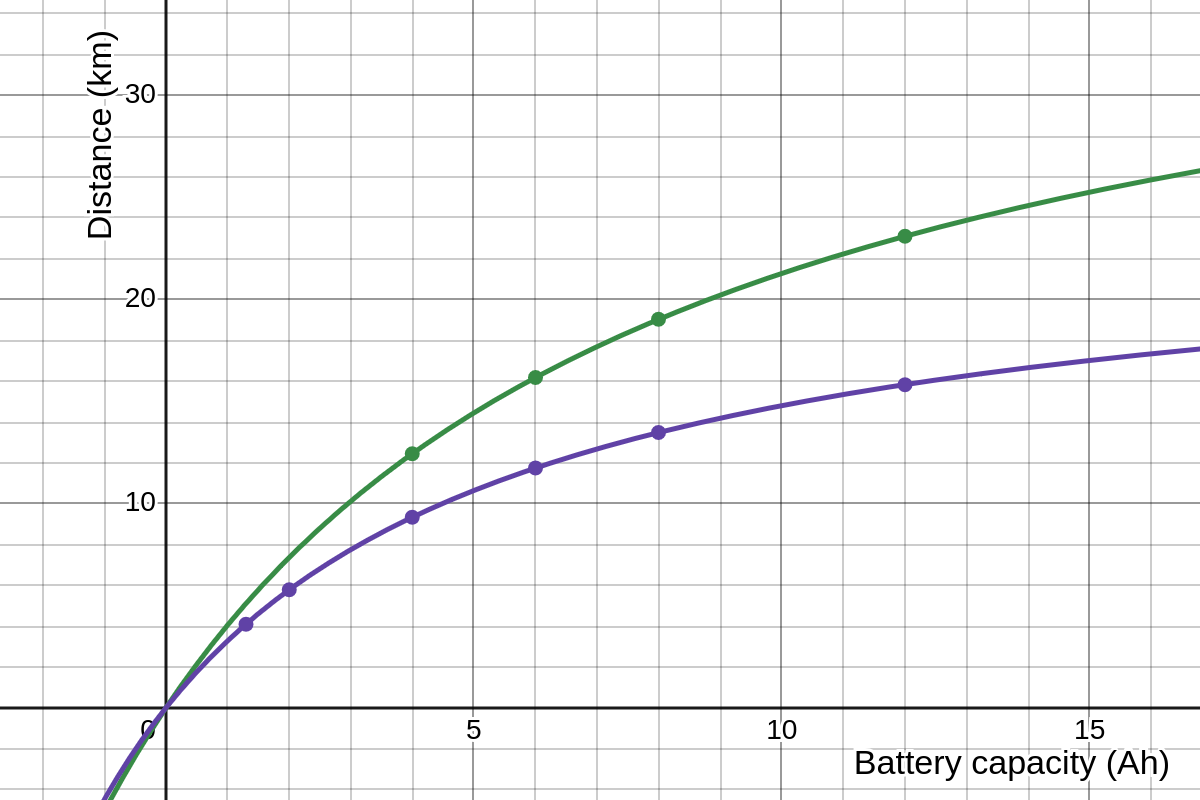
The graph below compares the performance of Li-ion (green) and LiPo (violet) batteries:
It is evident that LiPo batteries yield shorter distances compared to Li-ion batteries. This is expected since LiPo batteries are heavier and have a lower usable capacity, though they might offer advantages in fast-paced flight scenarios.
Conclusion
Optimizing drone battery selection is a balance between flight distance, weight, and specific performance needs. By accurately determining your drone’s constant $k_{drone}$ and applying the formulas above, you can make informed decisions tailored to your flying requirements.
Appendix: Doing the math
To choose the best battery, we want a formula that gives the distance in function of the battery capacity.
The assumption is that the drone transforms the battery capacity into lift, and lift energy consumption is proportional to the drone weight for a given speed.
At a given speed, the current $C$ needed to lift a drone is proportional to the drones’ mass $m$.
$$ k_{lift} = \frac{C}{m} \implies C = k_{lift} \cdot m $$
Then, integrating through time and assuming the thrust and current are constant:
$$ C \cdot t = k_{lift} \cdot m \cdot t $$
Assuming constant speed, the consumption is constant, and the consumed capacity is:
$$ Q_{consumed} = \int_0^t C dt = C \cdot t $$
Assuming constant speed $s$, we have:
$$ \mathrm{distance} = \int_0^t s dt = s \cdot t \implies t = \frac{\mathrm{distance}}{s} $$
Injecting the variables, we get:
$$ Q_{consumed} = k_{lift} \cdot m \cdot \frac{\mathrm{distance}}{s} $$
We now introduce a new constant $k_{drone} = \frac{s}{k_{lift}}$ (given a constant speed). It represents how the drone consumates energy to move. It is specific to the drone, the flight speed, and the effeciency of the drone (including propellers pitch and size, motors, etc), but does not depend on the drone’s mass. Rearranging the terms:
$$ \mathrm{distance} = k_{drone} \cdot \frac{Q_{consumed}}{m} $$
We now introduce the following terms:
- $Q$ is the total battery capacity, and $\eta$ is the fraction of the battery that can actually be used without damaging it, so that $Q_{consumed} = \eta \cdot Q$
- $m_e$ is the empty weight of the drone. It does not include the weight of the battery, but it does include everything the drone carries, including the HD camera. $m_b$ is the mass of the battery. So, $m = m_b + m_e$
- Assuming the mass of the battery is proportional to the battery capacity, $\rho$ is the mass per amp-hour. So, $m_e = \rho \cdot Q$, and $m = m_b + \rho \cdot Q$
With leads to the final formula:
$$ \mathrm{distance} = k_{drone} \cdot \frac{\eta \cdot Q}{m_e + \rho \cdot Q} $$
It can be plotted for $Q$, to determine the optimal battery capacity for our drone.